Advanced Data Structure

多维数组

• 数组的存储与定位

  行优先：C， 列优先：Fortran

  下标计算 ：

\[ \displaylines{ loc(A[j_0, ..., j_{n-1}]) = loc(A[0,...,0])\\ + size*[\sum_{i=0}^{n-2}(j_i\prod_{k=i+1}^{n-1}d_k)+j_{n-1}] } \]

• 特殊矩阵的压缩存储

  • 对称矩阵
  • 对角矩阵：只需存储N个对角元。
  • 上/下三角矩阵：\(N(N+1)/2+1\)
  • 稀疏矩阵：三元组表，十字链表

Generalized Lists （广义表，Multi-list）

线性表的拓展，线性表内的元素均为同一类型。

一个广义表的每个元素可以是子表（sub-list）或原子（atom）。

广义表深度：嵌套的最多子表数，所有元素化解为原子后的括号层数。

HEAD: 广义表中第一个(!)元素(!)。

TAIL: 广义表中第一个元素以外的元素构成的(!)广义表(!)。

​ eg. L = ((a,b),c), c = H(T(L)), b=H(T(H(L)))

• 线性表（sequential list）

  等价于一棵深度为1的树。

• 纯表（pure list）

  从根节点到任意一个叶节点只有一条路径，即任何元素只出现一次。等价于一棵树。

• 可重入表/再入表

  元素可以重复，但不包含回路。等价于DAG。深度定义同上。

• 循环表/递归表

  可以包含回路。等价于图。无法计算深度。

  eg. (L1:(L2:(L1, a)))

             *
            /
           L1
          ^ \
          |__L2
              \ 
               a
  

字典树 Trie

• 英文字母Trie树

  用于多子串的字符串匹配问题。

  Trie树往往不平衡。

• 二叉Trie树（PAT-Tree， Patricia）

二叉排序树变体 BST Variants

最佳BST

• N个关键码的集合构成N!种排列。

  其中只有\(Catalan(N) = \frac {C_{2n}^n}{n+1}\)个排列可以构成BST。

• BST查找效率的测量

  对BST扩充，则外部节点即查找失败的位置。

  最佳BST：根据用户历史访问频率，可以计算ASL最小的BST。

构造最佳BST的方法

• 节点检索等概率

  p为内部节点，共n个；q为外部节点，共n+1个。

\[ \displaylines{ \frac {p_i} W = \frac {q_j} W = \frac 1 {2n+1} \\ ASL(n) = \frac 1 {2n+1} (\sum_{i=1}^n(H(p_i)+1)+\sum_{j=0}^nH(q_j)) \\ = \frac 1 {2n+1} (I+n+E)\\ = \frac {2I+3n} {2n+1} } \]

​ 故在n已知时，构造I最短的BST即可，即类似完全二叉树的形状。

* 节点检索不等概率

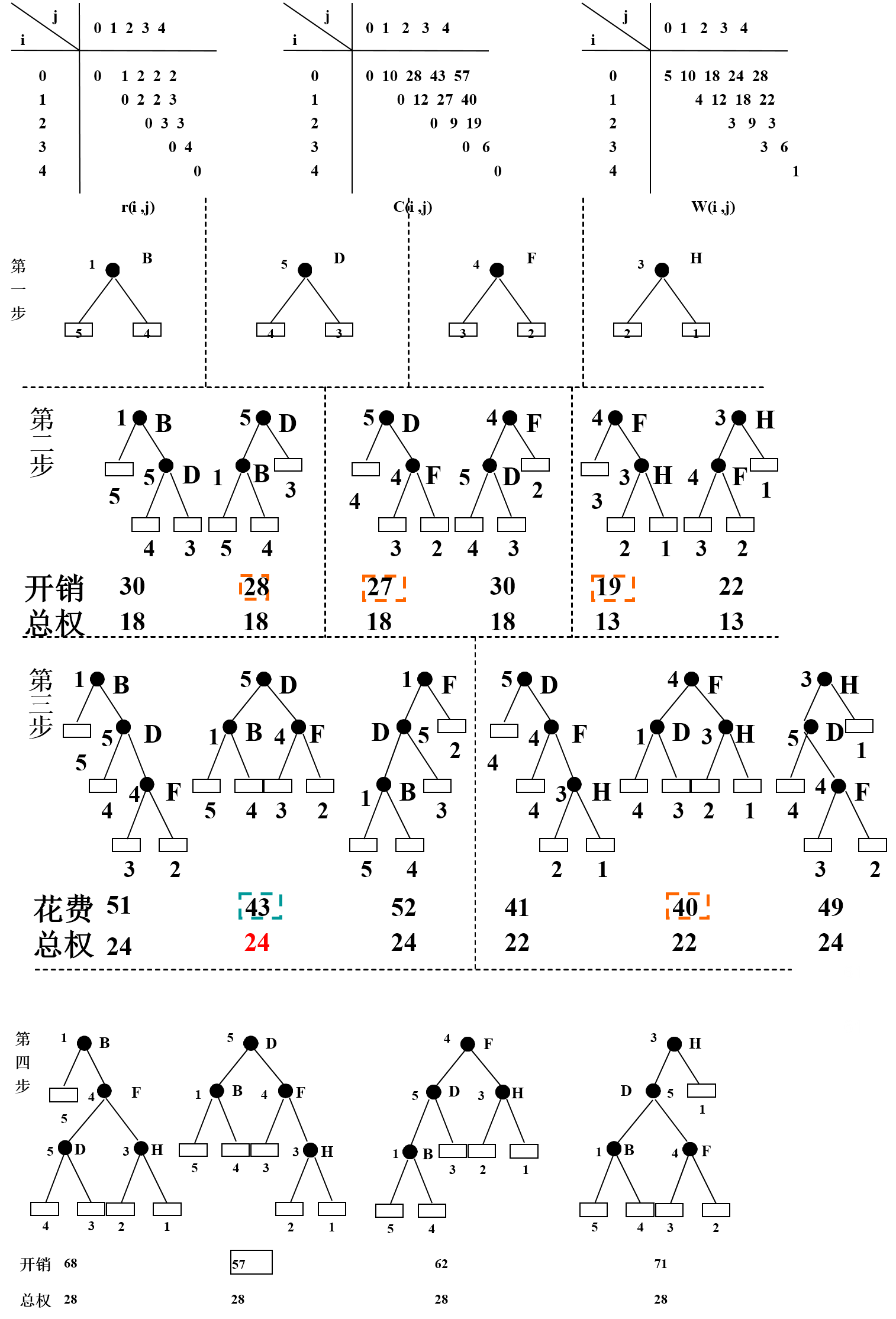
动态规划构造，任何子树都是最佳BST。

`t(i, j)`: 包含内部节点i+1到j的子树

`C(i, j)`: 节点i+1到j查询代价

`W(i, j)`: 权值总和，i+1到j的内部节点权重加上i到j外部节点的权重。

递推公式：

`C(i, j) = W(i, j) + min{C(i, k-1) + C(k, j)}, for k in [i, j]`

平衡BST（AVL）

平衡因子

bf(x) = height(rightchild(x))-height(leftchild(x))

AVL树的所有节点bf值只能是{0, 1, -1}。

\(ASL = O(lg n)\).

性质

• 空二叉树是AVL树
• T为AVL树，则左右子树L，R也是AVL树，且\(|h_R-h_L|\le1\)。
• T的高度为\(O(lg n)\)。

AVL插入

# TL;DR
先根据BST规则找到插入位置，并插入，回溯两层父节点检查bf。
* 仍平衡：结束
* 失衡：
    * LL，RR型：单旋转
    * LR，RL型：双旋转（提升最尾节点）

# 双旋转是坠简单的！排成一排，提升尾节点就平衡啦！

先根据BST规则找到插入位置。

• 插入发生偏重，但仍然平衡

• 插入前有偏重，插入后平衡

• 插入后失衡，进行平衡调整

  从新插入的节点u向上查找到第一个不平衡的祖先A，设A指向u的路径第一个子节点为B，第二个子节点为C。

  • 单旋转

    • LL：A的L的L导致失衡，bf(A)=-2

    # ===== init =====
              A(-2)
              /    \
         B(-1)   [h]T2
         /    \
    *T0[h+1]* [h]T1
    
    # ===== rotate A,B =====
             B(0)
             /    \
        T0[h+1]    A(0)
                  /    \
              T1[h]    [h]T2
    

  • RR：A的R的R导致失衡，bf(A)=2

  • 双旋转

    最终效果：先把四个子树排成一行，再把C挪到最上面，AB放中间。

    • LR：A的L的R导致失衡，bf(A)=-2

    # ===== init =====
                A(-2)
               /     \
            B(1)     [h]E
           /    \
        D[h]    (-1)C
                /   \
            *F[h]*  [h-1]G
    
    # ===== rotate B,C =====
                A(-2)
               /     \
            C(-2)    [h]E
           /    \
        B(0)    [h-1]G
       /   \
    D[h]   [h]F
    
    # ===== rotate A,C =====
                 C(0)
               /      \
              /         \
            B(0)         (1)A
           /    \        /   \
        D[h]    [h]F  G[h-1] [h]E
    

    • RL：A的R的L导致失衡，bf(A)=2

AVL删除

# TL;DR
如果是中间节点，先与前驱/后继交换位置，删除之，再向上两层检查父节点T的bf。
* 平衡：
    * 高度不变：结束
    * 高度减一：递归向上，检查bf
* 失衡：
    设父节点高子树R，讨论其bf：
    * bf(R)==0：单旋转RT，结束
    * bf(R)与bf(T)同号: 单旋转RT，递归向上
    * bf(R)与bf(T)异号：双旋转LR、R，LR、T；递归向上

先与后继（右子树最小值）或前驱（左子树最大值）交换再进行删除。

设被删节点的父节点为root。可能需要向上回溯 (modified = True)。

• bf(root) = 0

  左子树/右子树被缩短，bf = 1/-1，modified = False

• bf(root) != 0，且较高子树被缩短

  bf=0，modified=True（树高减一），故回溯向上检查父节点bf。

• bf(root) != 0，且较低子树被缩短

  开始时bf(root) =1/-1，不妨设较高子树为right，则bf(root)=1。

  • bf(right) = 0

    单旋转root，right；modified=False

    # ===== init =====
            T(1)        :[h+2]
            /   \
          [h]   (0)R
                /  \
              [h]   [h]
    # ===== delete =====
            T(2)        :[h+2]
            /   \
        [h-1]   (0)R
                /  \
              [h]   [h]
    # ===== rotate T,R =====
            R(-1)       :[h+2]
            /   \
         T(1)    [h]
          /  \
       [h-1]  [h]
    

  • bf(right) == bf(root)

    单旋转root，right；modified=True（树高减一），回溯。

    # ===== init =====
            T(1)        :[h+2]
            /   \
         [h]    (1)R
                /  \
            [h-1]   [h]
    
    # ===== delete =====
            T(2)        :[h+2]
            /   \
        [h-1]   (1)R
                /  \
            [h-1]   [h] 
    
    # ===== rotate T,R =====
            R(0)        :[h+1], backtrace
            /   \
         T(0)    [h]
         /   \
     [h-1]   [h-1]
    

  • bf(right) != bf(root)

    双旋转RL，R；root，RL；modified=True（树高减一），回溯。

    ### based on condition of LR(left of right):
    ## bf(LR)=0
    # ===== init =====
              T(1)          :[h+2]
             /    \
          [h]      (-1)R
                  /   \
              LR(0)    [h-1]
              /   \
          [h-1]   [h-1]
    # ===== delete =====
              T(2)
             /    \
        [h-1]      (-1)R
                  /   \
              LR(0)    [h-1]
              /   \
          [h-1]   [h-1]
    
    # ===== double rotate =====
                 LR(0)          :[h+1], backtrace
               /       \
              /          \
            T(0)         (0)R
           /    \        /   \
        [h-1]   [h-1] [h-1]  [h-1]
    
    
    ## bf(LR)=1
    # ===== init =====
              T(1)
             /    \
          [h]      (-1)R
                  /   \
              LR(1)    [h-1]
              /   \
          [h-2]   [h-1]   
    # ===== delete =====
              T(2)
             /    \
        [h-1]      (-1)R
                  /   \
              LR(1)    [h-1]
              /   \
          [h-2]   [h-1]   
    # ===== double rotate =====
                 LR(0)
               /       \
              /          \
            T(-1)        (0)R
           /    \        /   \
        [h-1]   [h-2] [h-1]  [h-1]
    
    
    ## bf(LR)=-1
    # ===== init =====
              T(1)
             /    \
          [h]      (-1)R
                  /   \
              LR(-1)   [h-1]
              /   \
          [h-1]   [h-2]
    # ===== delete =====
              T(2)
             /    \
        [h-1]      (-1)R
                  /   \
              LR(1)    [h-1]
              /   \
          [h-1]   [h-2]  
    # ===== double rotate =====
                 LR(0)
               /       \
              /          \
            T(0)         (1)R
           /    \        /   \
        [h-1]   [h-1] [h-2]  [h-1]
    

伸展树（Splay）

动态自组织的数据结构，检索频繁的记录离根节点更近。

Splay规则保证访问代价较低，不保证平衡。

展开 Splaying

访问节点X时，进行展开操作：

• 插入/检索X：把X移动到BST根节点。
• 删除X：先与前驱/后继交换，删除后，把此时X的父节点移动到BST根节点。

具体而言：

• X是根节点的直接子节点：单旋转

• X离根节点两层及以上：一系列双旋转+可能的单旋转

  • 一字型旋转：LL/RR，同构调整。仅仅把X向上提升。

    快速做法：双重单旋转

    # ===== insert C =====
            A
           / \
          B   D
         / \
        C   E
    # ===== rotate AB =====
            B
           / \
          C   A
             / \
            E   D
    # ===== rotate BC =====
            C
             \
              B
               \
                A
               / \
              E   D
    

    注意！Splay默认自顶向下的进行旋转：

    # ===== insert 6 =====
        8
       / 
      7
     /
    6
    # ===== rotate 8,7 =====
        7
       / \
      6   8
    
    # ===== rotate 7,6 =====
       6
        \
         7
          \
           8
    
    ## another method, **Don't use this!!!**
    # ===== rotate 6,7 =====
       8
      /
     6
      \
       7
    # ===== rotate 8,6 =====
       6
        \
         8
        /
       7
    

  • 之字形旋转：LR/RL，异构调整。提升X的同时，子树高度减一，趋近平衡。

    快速做法：这个就是双旋转，可以直接排一排、提升尾。

效率分析

• 一次访问操作的代价：\(O(n)\)，不保证单个操作高效。

• m次访问操作的总代价：\(O(mlgn)\)，每次操作平均代价\(O(lgn)\)，保证多个操作平均高效。