Network flow 2

有流量下界的最大流

把每一条有下界的边分为必要边+不必要边。

• Budget

最小费用最大流

每条边有一个单位流量所需的费用，求所有最大流中费用最小的。

• Farm Tour

二部图最大匹配

左半部分无限边(1边也可以)连接对应的右半部分，超源点用1边连向所有左半部分，超汇点用1出边连接所有右半部分。调用最大流即可得到最大匹配数。

另一个解决二部图最大匹配问题的算法是匈牙利算法。

• The perfect stall

  #include <iostream>
  #include <deque>
  #include <cstring>
  #include <algorithm>
  
  using namespace std;
  
  const int inf = 0x3f3f3f3f;
  const int maxv = 500;
  int V, E, s, t;
  
  int G[maxv][maxv]; // adjancency matrix
  int vis[maxv], dep[maxv];
  
  bool bfs() {
    int depth = 0;
    deque<int> q;
    memset(dep, -1, sizeof(dep));
    dep[s] = 0;
    q.push_back(s);
    while (!q.empty()) {
        int u = q.front(); q.pop_front();
        for (int i = 0; i < V; i++) {
            if (G[u][i] > 0 && dep[i] == -1) {
                dep[i] = dep[u] + 1;
                if (i == t) return true;
                else q.push_back(i);
            }
        }
    }
    return false;
  }
  
  int dinic() {
    int mxflow = 0;
    deque<int> q;
    while (bfs()) {
        q.push_back(s);
        memset(vis, 0, sizeof(vis));
        vis[s] = 1;
        while (!q.empty()) {
            int u = q.back();
            // u is target
            if (u == t) {
                int mnflow = inf;
                int v; // mnflow_start_vertex
                for (int i = 1; i < q.size(); i++) {
                    int vs = q[i - 1];
                    int ve = q[i];
                    if (G[vs][ve] > 0 && mnflow > G[vs][ve]) {
                        mnflow = G[vs][ve];
                        v = vs;
                    }
                }
                for (int i = 1; i < q.size(); i++) {
                    int vs = q[i - 1];
                    int ve = q[i];
                    G[vs][ve] -= mnflow;
                    G[ve][vs] += mnflow;
                }
                mxflow += mnflow;
                // pop back 
                while (!q.empty() && q.back() != v) {
                    vis[q.back()] = 0;
                    q.pop_back();
                }
            }
            // u is not target
            else {
                // only add one point in the next layer to stack.
                bool found = false;
                for (int i = 0; i < V; i++) {
                    if (G[u][i] > 0 && dep[i] == dep[u] + 1 && !vis[i]) {
                        vis[i] = 1;
                        q.push_back(i);
                        found = true;
                        break;
                    }
                }
                // can't find such point.
                if (!found) q.pop_back();
            }
        }
    }
    return mxflow;
  }
  
  int N, M, a, b;
  
  int main() {
    while (cin >> N >> M) {
        V = N + M + 2;
        s = V - 2;
        t = V - 1;
        memset(G, 0, sizeof(G));
        for (int i = 0; i < N; i++) {
            cin >> a;
            for (int j = 0; j < a; j++) {
                cin >> b;
                G[i][N + b - 1] = inf;
            }
        }
        for (int i = 0; i < N; i++) G[s][i] = 1;
        for (int i = N; i < N + M; i++) G[i][t] = 1;
        cout << dinic() << endl;
    }
  }
  

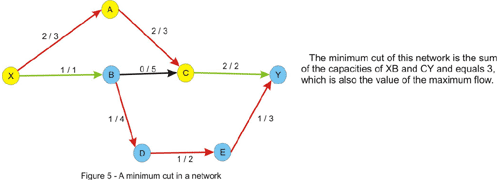
最小割

最大流==最小割。