String

char

• 偏序编码规则：

  根据字符的自然定义，某些字符间两两可以比较次序。（一般为字典序）

string

• 存储

  • 静态：顺序，c标准字符串。
  • 动态：String类。

• 方法

  • 标准字符串

    char* s[L] // capacity is L-1. ('\0' is reserved for the last place.)
    int strlen(char* s)
    char* strstr(char* str1, char* str2) // find str2 in str1, if not found, return NULL
    char* strcpy(char* to, char* from)  // return `to`
    char* strcat(char* to, char* from)
    int strcmp(char* a, char* b)  // 0 for ==
    char* strchr(char* s, char c)  // find c in s (left to right), return &s[i] or '\0'
    char* strrchr(char* s, char c)  // right to left
    

  • class string

    string s; // empty string
    s2 = s.substr(start, count); // shrink count automatically
    s3 = s + s2;
    int l = s.length();
    string s = string(1, 'a'); // single char to string. to_string() is wrong.
    string s = to_string(123); // s="123"
    s[0] = 'r' // mutable
    int a = stoi(s); // stof, stoll, stod, ...
    s.find(s2) // int index to s2, or -1 if not found
    

Pattern Matching

• Classification

  • Exact Matching

    Single Matching, Ambiguous (Wild-Card), Regular Expression.

  • Approximate Matching

    Edit Distance: Insertion, Deletion, Replacement.

    (Genomic Alignment)

• Algorithms

  Assuming Target length is \(n\), Pattern length is \(m\).

  • Brute Force

    Time: \(O(nm)\)

    int BF(string t, string p){
        int i,j;
        for(i=0; i<t.length()-p.length(); i++){
            for(j=0, j<p.length()&&t[i+j]==p[j]; j++) ;
            if(j==p.length()) return i;
        }
        return -1;
    }
    

  • KMP

    **Time: \(O(m+n)\). **

    No back-tracing match.

    Why k = next[k]: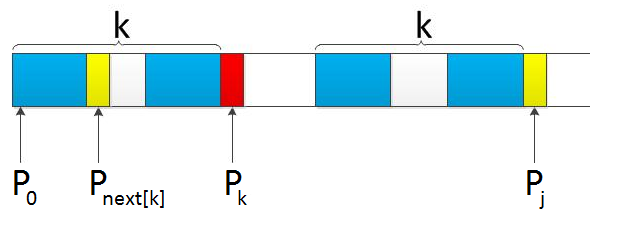

    

    /*******************************
    * What is next[i] ?
    *    length of Longest Commen Prefix & Postfix of [0,i-1]
    *    可以重叠，但不能完全重叠。
    *    eg.非优化的aaaaa ：-1 0 1 2 3
    * How to get next[i] RECURSIVEly ?
    *    p[i] == p[k] --> next[i+1] = next[i] + 1;
    *    else --> let k = next[k], check again.
    *******************************/
    #include <iostream>
    #include <string>
    using namespace std;
    
    int* getNext(string p) {
        int l = p.length();
        int* next = new int[l];
        next[0] = -1;
        int i = 0, k = -1;
        while (i < l - 1) {
            while (k >= 0 && p[k] != p[i]) k = next[k];
            i++, k++;
            if (p[k] == p[i]) next[i] = next[k]; // Enhancement.
            else next[i] = k;
        }
        return next;
    }
    
    int KMP(string t, string p){
        int tlen = t.length();
        int plen = p.length();
        if (tlen < plen) return -1;
        int* next = getNext(p);
        int i = 0, j = 0;
        while (i < tlen && j < plen){
            if (j == -1 || t[i] == p[j]) i++, j++;
            else j = next[j];  //重新对齐后，仍要比较一次i位置
        }
        if (j == plen) return i-j;
        else return -1;
    }
    

    KMP的总比对次数：母串长度+失配次数

    Examples of KMP:

    index	0	1	2	3	4	5
    string	a	b	a	c	a	b
    next	-1	0	0	1	0	1/0

    如何目测改进版Next数组：

    先目测原始Next数组，之后逐位比较p[i]==p[next[i]] ? next2[i]=next2[next[i]] : next2[i]=next[i].

    注意是next2[next[i]]。

    eg.

    index	0	1	2	3	4	5
    string	a	a	b	a	a	c
    next	-1	0	1	0	1	2
    next2	-1	-1	1	-1	-1 (not 0!)	2

    eg.

    index	0	1	2	3	4	5	6	7	8	9
    string	a	b	c	d	a	a	b	c	a	b
    next	-1	0	0	0	0	1	1	2	3	1
    next2	-1	0	0	0	-1	1	0	0	3	0

Boyer-Moore 算法

实际上Ctrl+F，GNU grep使用的算法，预处理O(m)，平均查找O(n/m)，最坏O(n)，NB！

坏字符原则+好后缀原则。每次失配时，根据这两个规则中后移位数大的移动。

理解比较容易，但感觉在实现上有一些trick，所以不太适合教学。。？

http://blog.jobbole.com/52830/

http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html